nLab type I string theory
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Quantum field theory
Higher spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Elliptic cohomology
Contents
Idea
What is called type I string theory is type IIB string theory on orientifold spacetimes, hence on O9-planes.
Its T-dual, called type I’ string theory, is type IIA string theory on O8-planes, which under the duality between M-theory and type IIA string theory is M-theory KK-compactified on the orientifold (see also M-theory on S1/G_HW times H/G_ADE):
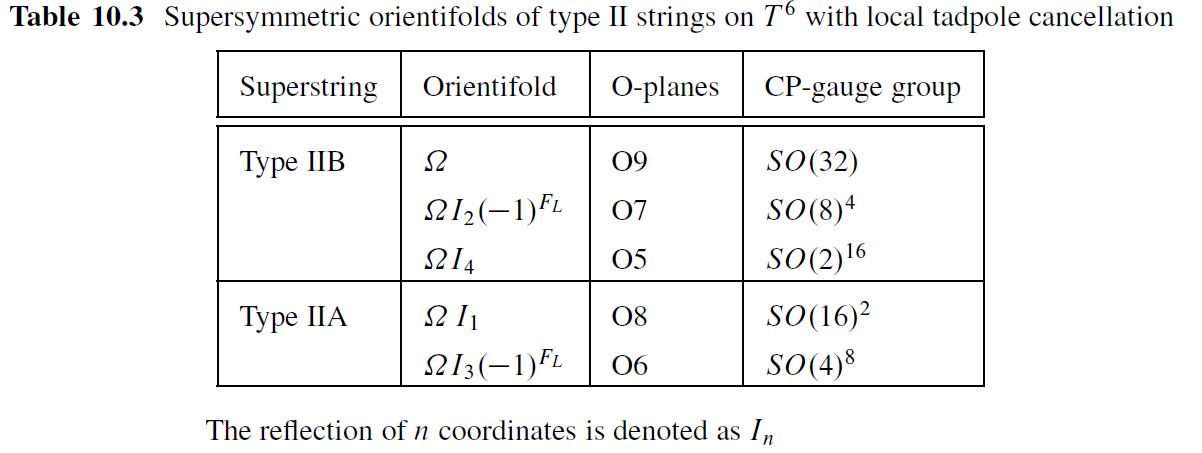
table from BLT 13
Properties
Tadpole cancellation and -GUT in Type I
For type I string theory on flat (toroidal) target spacetime orientifolds (i.e. for type IIB string theory on flat toroidal O9-planes) RR-field tadpole cancellation requires 32 D-branes (see this Remark for counting D-branes in orientifolds) to cancel the O-plane charge of -32 (here).
Under the duality between type I and heterotic string theory this translates to the semi-spin gauge group SemiSpin(32) of heterotic string theory.
Discussion of type-I string phenomenology and grand unified theory based on SO(32) type-I strings: (MMRB 86, Ibanez-Munoz-Rigolin 98, Yamatsu 17).
Tadpole cancellation and -GUT in Type I’
For type I’ string theory on flat (toroidal) target spacetime orientifolds (i.e. for type IIA string theory on two flat toroidal O8-planes) RR-field tadpole cancellation requires 16 D-branes (see this Remark for counting D-branes in orientifolds) on each of the two O8-planes to cancel the total O-plane charge of (here).
Discussion of Spin(16)-GUT phenomenology:
(…)
Orbifolds of type I
Type I’ on toroidal orientifolds with ADE-singularities (e.g. Bergman&Rodriguez-Gomez 12, Sec. 3)
dual to heterotic M-theory on ADE-orbifolds.
(…)
Dualities
String-string dualities
See at duality between type I and heterotic string theory
Horava-Witten theory
One considers the KK-compactification of M-theory on a Z/2-orbifold of a torus, hence of the Cartesian product of two circles
such that the reduction on the first factor corresponds to the duality between M-theory and type IIA string theory, hence so that subsequent T-duality along the second factor yields type IIB string theory (in its F-theory-incarnation). Now the diffeomorphism which exchanges the two circle factors and hence should be a symmetry of M-theory is interpreted as S-duality in type II string theory:

graphics taken from Horava-Witten 95, p. 15
If one considers this situation additionally with a -orbifold quotient of the first circle factor, one obtains the duality between M-theory and heterotic string theory (Horava-Witten theory). If instead one performs it on the second circle factor, one obtains type I string theory.
Here in both cases the involution action is by reflection of the circle at a line through its center. Hence if we identify then the action is by multiplication by /1 on the real line.
In summary:
M-theory on
-
yields heterotic string theory
-
yields type I' string theory
Hence the S-duality that swaps the two circle factors corresponds to a duality between heterotic E and type I’ string theory. And T-dualizing turns this into a duality between type I and heterotic string theory.

graphics taken from Horava-Witten 95, p. 16
Related concepts
cohomology theories of string theory fields on orientifolds
References
General
-
Luis Ibáñez, Angel Uranga, section 4.4.3 of: String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012
-
Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Section 9.4 and 10.6 of: Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics, Springer 2013
Relation to M-theory (via Horava-Witten theory):
-
Petr Hořava, Edward Witten, Heterotic and Type I string dynamics from eleven dimensions, Nucl. Phys. B460 (1996) 506 (arXiv:hep-th/9510209)
-
Petr Hořava, Edward Witten, Eleven dimensional supergravity on a manifold with boundary, Nucl. Phys. B475 (1996) 94 (arXiv:hep-th/9603142)
A comprehensive discussion of the (differential) cohomological nature of general type II/type I orientifold backgrounds is in
- Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)
with details in
-
Daniel Freed, Lectures on twisted K-theory and orientifolds (pdf)
-
Jacques Distler, Dan Freed, Greg Moore, Spin structures and superstrings, Surveys in Differential Geometry, Volume 15 (2010) (arXiv:1007.4581, doi:10.4310/SDG.2010.v15.n1.a4)
Related lecture notes / slides include
-
Jacques Distler, Orientifolds and Twisted KR-Theory (2008) (pdf)
-
Daniel Freed, Dirac charge quantiation, K-theory, and orientifolds, talk at a workshop Mathematical methods in general relativity and quantum field theories, November, 2009 (pdf)
-
Greg Moore, The RR-charge of an orientifold, Oberwolfach talk 2010 (pdf, pdf, ppt)
Type I’
Original articles on type I' string theory:
-
John Schwarz, Some Properties of Type I’ String Theory, in: Mikhail Shifman (ed.), The Many Faces of the Superworld, pp. 388-397 (2000) (arXiv:hep-th/9907061, doi:10.1142/9789812793850_0023)
-
Justin R. David, Avinash Dhar, Gautam Mandal, Probing Type I’ String Theory Using D0 and D4-Branes, Phys. Lett. B415 (1997) 135-143 (arXiv:hep-th/9707132)
Type I’ on toroidal orientifolds with ADE-singularities (dual to heterotic M-theory on ADE-orbifolds):
- Oren Bergman, Diego Rodriguez-Gomez, 5d quivers and their duals, JHEP07 (2012) 171 (arxiv:1206.3503)
Phenomenology
Type I string phenomenology and discussion of GUTs based on SO(32) type I strings (see also at heterotic phenomenology):
-
H.S. Mani, A. Mukherjee, R. Ramachandran, A.P. Balachandran, Embedding of GUT in superstring theories, Nuclear Physics B Volume 263, Issues 3–4, 27 January 1986, Pages 621-628 (arXiv:10.1016/0550-3213(86)90277-4)
-
Luis Ibáñez, C. Muñoz, S. Rigolin, Aspects of Type I String Phenomenology, Nucl.Phys. B553 (1999) 43-80 (arXiv:hep-ph/9812397)
-
Emilian Dudas, Theory and Phenomenology of Type I strings and M-theory, Class. Quant. Grav.17:R41-R116, 2000 (arXiv:hep-ph/0006190)
-
Naoki Yamatsu, String-Inspired Special Grand Unification, Progress of Theoretical and Experimental Physics, Volume 2017, Issue 10, 1 (arXiv:1708.02078, doi:10.1093/ptep/ptx135)
Duality
Discussion of duality with heterotic string theory includes the following.
The original conjecture is due to
- Edward Witten, section 5 of String Theory Dynamics In Various Dimensions, Nucl.Phys.B443:85-126 (1995) (arXiv:hep-th/9503124)
More details are then in
- Joseph Polchinski, Edward Witten, Evidence for Heterotic - Type I String Duality, Nucl.Phys.B460:525-540,1996 (arXiv:hep-th/9510169)
Geometric engineering of SCFT
On D=6 N=(1,0) SCFTs via geometric engineering on M5-branes/NS5-branes at D-, E-type ADE-singularities, notably from M-theory on S1/G_HW times H/G_ADE, hence from orbifolds of type I' string theory (see at half NS5-brane):
-
Michele Del Zotto, Jonathan Heckman, Alessandro Tomasiello, Cumrun Vafa, 6d Conformal Matter, JHEP02(2015)054 (arXiv:1407.6359)
-
Davide Gaiotto, Alessandro Tomasiello, Holography for theories in six dimensions, JHEP12(2014)003 (arXiv:1404.0711)
-
Kantaro Ohmori, Hiroyuki Shimizu, Compactifications of 6d Theories and Brane Webs, J. High Energ. Phys. (2016) 2016: 24 (arXiv:1509.03195)
-
Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams, JHEP05 (2019)203 (arXiv:1509.03300)
-
Ibrahima Bah, Achilleas Passias, Alessandro Tomasiello, compactifications with punctures in massive IIA supergravity, JHEP11 (2017)050 (arXiv:1704.07389)
Sugimoto string theory
What is now called Sugimoto string theory is a non-supersymmetric version of type I string theory, given by 10d type IIB string theory on an orientifold (instead of ), hence with RR-field tadpole cancellation by 32 anti D9-branes (instead of plain D9-branes), whose gauge group is the symplectic group .
The original article:
- Shigeki Sugimoto: Anomaly Cancellations in the Type I D9-anti-D9 System and the String Theory, Prog. Theor. Phys. 102 (1999) 685-699 [arXiv:hep-th/9905159, doi:10.1143/PTP.102.685]
Further discussion:
-
Sanefumi Moriyama: String as Spontaneously Supersymmetry Broken Theory, Phys. Lett. B 522 (2001) 177-180 [arXiv:hep-th/0107203, doi:10.1016/S0370-2693(01)01278-3]
-
Hector Parra de Freitas, p. 166 of: String Compactifications with Half-maximal Supersymmetry, PhD thesis, Université Paris-Saclay (2023) [hal/tel-04234221, pdf]
-
Vittorio Larotonda, Ling Lin: Anomaly Inflow and Gauge Group Topology in the 10d Sugimoto String Theory [arXiv:2412.17894]
Last revised on December 27, 2024 at 17:34:17. See the history of this page for a list of all contributions to it.